Решение показательных уравнений

Решение показательных уравнений продолжим рассмотрением уравнений, содержащих степени с одинаковыми основаниями и противоположными показателями.

В общем виде показательные уравнения такого вида можно записать так:

${k_1}{a^{f(x)}} + {k_2}{a^{ - f(x)}} + {k_3} = 0,$

где

$a,{k_1},{k_2},{k_3} -$

числа, причём a>0, a≠1.

Проще всего решить это уравнение сведением к квадратному. Для этого обе части уравнения умножим на степень с положительным показателем. Потери корней не происходит, так как

${a^{f(x)}} > 0.$

${k_1}{a^{f(x)}} + {k_2}{a^{ - f(x)}} + {k_3} = 0\_\_\_\left| { \cdot {a^{f(x)}}} \right.$

${k_1}{a^{f(x) + f(x)}} + {k_2}{a^{ - f(x) + f(x)}} + {k_3} \cdot {a^{f(x)}} = 0$

${k_1}{a^{2f(x)}} + {k_2}{a^0} + {k_3} \cdot {a^{f(x)}} = 0$

Так как a⁰=1, получаем показательное уравнение, сводящееся к квадратному:

${k_1}{a^{2f(x)}} + {k_3} \cdot {a^{f(x)}} + {k_2} = 0.$

Рассмотрим примеры решения уравнений такого вида.

$1){3^x} + {3^{2 - x}} = 10$

Умножим почленно обе части уравнения на 3 в степени x:

${3^x} + {3^{2 - x}} = 10\_\_\_\left| { \cdot {3^x}} \right.$

${3^{x + x}} + {3^{2 - x + x}} = 10 \cdot {3^x}$

${3^{2x}} + {3^2} = 10 \cdot {3^x}$

${3^{2x}} - 10 \cdot {3^x} + 9 = 0.$

Пусть

${3^x} = t,t > 0,$

тогда

${t^2} - 10t + 9 = 0$

Корни этого квадратного уравнения — t1=9, t2=1 — оба удовлетворяют условию t>0. Возвращаясь к исходной переменной, получаем простейшие показательные уравнения:

${3^x} = 9;{3^x} = 1$

${3^x} = {3^2};{3^x} = {3^0}$

$x = 2;x = 0.$

Ответ: 2; 0.

$2){10^{1 + {x^2}}} - {10^{1 - {x^2}}} = 99$

Обе части уравнения умножим почленно на 10 в степени x²:

${10^{1 + {x^2}}} - {10^{1 - {x^2}}} = 99\_\_\_\left| { \cdot {{10}^{{x^2}}}} \right.$

${10^{1 + {x^2} + {x^2}}} - {10^{1 - {x^2} + {x^2}}} = 99 \cdot {10^{{x^2}}}$

$10 \cdot {10^{2{x^2}}} - {10^1} - 99 \cdot {10^{{x^2}}} = 0$

Замена

${10^{{x^2}}} = t,t > 0,$

приводит к квадратному уравнению

$10{t^2} - 99t - 10 = 0$

Из двух его корней — t1=10 и t2= -0,1 — только первый удовлетворяет условию t>0. Обратная замена

${10^{{x^2}}} = 10$

${x^2} = 1$

$x = \pm 1.$

Ответ: ±1.

$3){5^{{{\sin }^2}x}} + {5^{{{\cos }^2}x}} = 6$

Согласно основному тригонометрическому тождеству,

${\sin ^2}x + {\cos ^2}x = 1, \Rightarrow {\cos ^2}x = 1 - {\sin ^2}x$

Отсюда

${5^{{{\sin }^2}x}} + {5^{1 - {{\sin }^2}x}} = 6\_\_\_\left| \cdot \right.{5^{{{\sin }^2}x}}$

${5^{{{\sin }^2}x + {{\sin }^2}x}} + {5^{1 - {{\sin }^2}x + {{\sin }^2}x}} = 6 \cdot {5^{{{\sin }^2}x}}$

${5^{2{{\sin }^2}x}} + {5^1} - 6 \cdot {5^{{{\sin }^2}x}} = 0$

Замена

${5^{{{\sin }^2}x}} = t,t > 0$

Квадратное уравнение

${t^2} - 6t + 5 = 0$

имеет два корня t1=5 и t2=1. Оба корня удовлетворяют условию t>0. Обратная замена

${5^{{{\sin }^2}x}} = 5;{5^{{{\sin }^2}x}} = 1$

${\sin ^2}x = 1;{\sin ^2}x = 0$

$\sin x = \pm 1;\sin x = 0$

Это — простейшие тригонометрические уравнения.

$x = \frac{\pi }{2} + \pi n,n \in Z;$

$x = \pi k,k \in Z.$

Отметим полученные семейства решений на единичной окружности:

$n = 0,x = \frac{\pi }{2};n = 1,x = \frac{{3\pi }}{2};$

$k = 0,x = 0;k = 1,x = \pi$

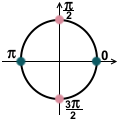Можно объединить два семейства решений в одно:

$x = \frac{{\pi n}}{2},n \in Z.$

Ответ:

$x = \frac{{\pi n}}{2},n \in Z.$

Степени

${a^{f(x)}},{a^{ - f(x)}}$

— взаимно-обратные (их произведение равно единице). Другой способ решения таких уравнений — непосредственная замена

${a^{f(x)}} = t$

и переход к дробному рациональному уравнению

${k_1}{t^2} + \frac{{{k_2}}}{t} + {k_3} = 0,$

которое, в свою очередь, также приводится к квадратному.

В следующий раз рассмотрим примеры решения показательных уравнений с взаимно-обратными степенями, основания которых — иррациональные числа.

Добавить комментарий Отменить ответ